目录

0x01 Why

目前流行的fuzzing（如AFL）通常使用较为简单的coverage information，这种覆盖的不准确和不完整给fuzzing带来了严重的局限性。首先，它会导致路径冲突，从而影响fuzzing挖掘出导致新崩溃的潜在路径。更重要的是，它也会影响fuzzing的最优决策。此外，学术界的大部分研究的是Coverage-guided fuzzing，很少有目光真正的投在Coverage上，所以CollAFL做了这一块的内容。

0x02 What

对AFL中的coverage inaccuracy 和seed选择策略做了改进，改进后的工具称为CollAFL

0x03 How

本文主要做了两个改进。第一，在AFL中，AFL要用到一个64KB bitmap来保存Coverage的信息，在AFL进行fuzzing的时候，会发生碰撞，两个快构成一个边，AFL为边赋了hash值，这个hash就代表这条边，可是不同的边计算出的hash可能是一样的，于是就发生了Collision ， Collision可能会导致某些input到达新的路径，但AFL却没有将该input作为seed，本文主要针对这一点，采用了一个新的算法，解决了路径hash collision问题。第二，在seed选择的时候，CollAFL会优先选择对Coverage有贡献的seed。

CollAFL的具体做法如下。

对于hash Collision问题。

在AFL中，给定边A->B，其hash算法如下：

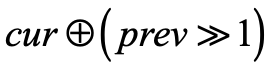
其中prev和cur分别是基本块A和B的key, 由于key的随机性，两个不同的边可能具有相同的hash值。于是CollAFL对其进行了改进，改进如下。
给定两个带有prev和curkey的块A和B，如下图所示：

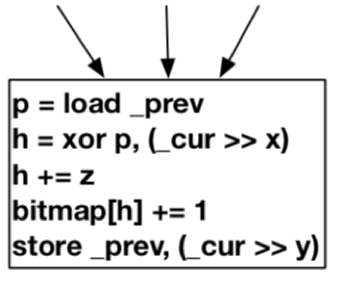
其hash算法如下：

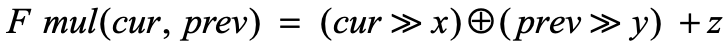
其中，<x，y，z>是要确定的参数，不同的边可能不同。AFL使用的公式是该算法的一种特殊形式，即对于所有边/块，
<x=0，y=1，z=0>。Fmul的计算过程与AFL相同，开销相同。

但是，此算法不能保证为给定的应用程序找到解决方案，因为应用程序中有太多的基本块，因此不能遍历所有可能的参数。即使可以这样做，也不能保证解决方案的存在，因为基本块的key是随机分配的。

因此，CollAFL进一步将所提出的hash计算算法改进如下：

• 具有Single Precedent块的hash算法

如果一个块只有一个Precedent块，如下图所示：

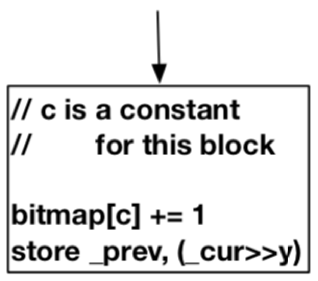
可以在结束块中直接为该边分配一个hash，算法如下：

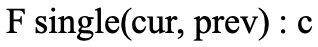
其中prev和cur是分配给块A和B的key，参数c是要确定的唯一常量。

• 具有Multiple Precedents块的hash算法

如果一个块B有Multiple Precedents块，如下图所示：

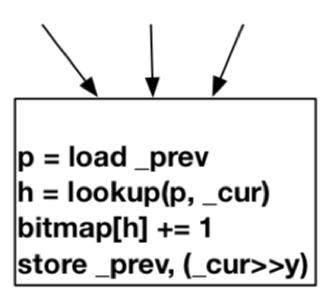
即如果B具有多个传入边缘，则必须动态计算块B中的hash，算法如下：

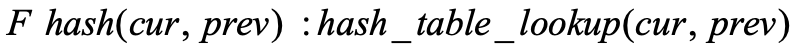
其中prev和cur是块A和块B的key，它构建了一个离线哈希表，所有边的唯一hash以unsolvable block结尾，不同于所有其他边的hash。在运行时，它查找这个预先计算的哈希表，以获取这些边的哈希值，并使用它们的起始块和结束块作为key。需要注意的是，在运行时，哈希表查找操作比以前的算法Fmul和Fsingle慢得多。

• 整体缓解方案

在确保bitmap size大于边数的情况下，根据不同的类型，使用Fmul、Fsingle和Fhash这三个hash计算公式，如下所示：

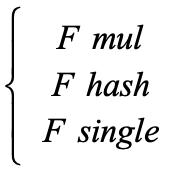
对于种子选择问题，CollAFL提供了三个选择策略。

• CollAFL-br

拥有更多未受影响的邻近分支的种子将优先于模糊，该策略使用未接触的临近分支数作为测试用例t的权重，计算公式如下：

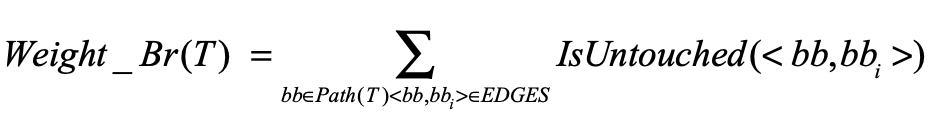
此公式只在且仅当边缘<bb,bb_i>未被任何先前的测试用例覆盖，否则为0。

通过此公式，可用权重来考虑种子的选择，即权重更高的种子将被优先考虑模糊化，值得注意的是，随着测试的进行，先前运行的测试用例集将发生变化，因此所接触的函数的返回值也将发生变化。因此，测试用例的权重是动态的。

• CollAFL-desc

拥有更多未受影响的邻近后代的种子将优先考虑模糊，该策略使用未接触的邻近后代的数量作为测试用例t的权重，计算公式如下：

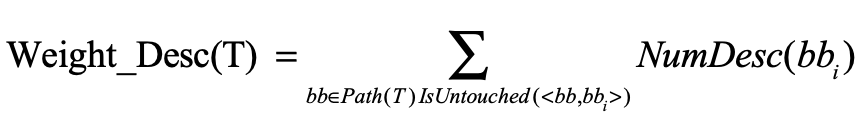
其中函数IsUntouched与CollAFL-br策略中使用的相同，函数NumDesc返回从参数基本块开始的子代路径数。其形式定义如下：

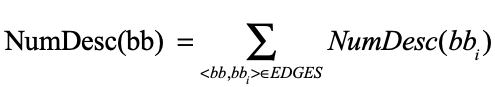
需要注意的是，这里的权重不是确定的，因为函数IsUntouched是动态的。但是，对于每个基本块，子路径的数量是确定的。

• CollAFL-mem

拥有更多内存访问操作的种子将优先于模糊，该策略使用内存访问操作的数量作为测试用例t的权重，其计算公式如下：

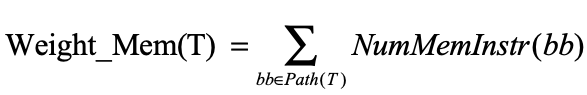
其中，函数NumMemInstr返回参数基本块中的内存访问操作数，可以静态计算。因此，与前两个策略不同，以这种方式计算的权重是确定性的。

以上策略，总的来说，第一个策略，考虑的是，每个种子会走一条路径，一条路径实际有不同分支的，有些分支是被其他种子测过，有的分支没有。然后CollAFL统计这个种子多样分支被测过，有多少分支没有被测过，于是就有可能出现两个种子。第一个种子有一个分支没测过，第二个种子有N个分支没测过。CollAFL选择的就是后者，因为在第二个进行变异的时候有非常大的概率，种子存在没有被触发、测试过的分支。

第二个策略是在第一个策略基础上的改进，策略一中的分支记为初始值，此处分支后面会跟着一些子路径，所以也要考虑子路径的数目，因此计数不再是初始值，而是把后面的分支根据路径数量加进来。

第三个策略，考虑的是内存访问，CollAFL统计这个种子所走的路径，基本块访问的数量，那些访问数量多的，优先级就相应高一点。

0x04 Result

• 在24个实际应用程序中发现了157个新的安全漏洞，其中95个被CVE确认。可惜的是，作者没有开源CollAFL

0x05 Question

确保bitmap size大于边数的原理？

答：上文中提到了AFL中的hash计算公式： ，在这个公式里，其计算结果能够保证小于等于cur或者prev的值，而cur或者prev 的值小于等于64k，bitmap 则可以认为是一个数组（如：bitmap[64]）， 前面边的hash值的计算结果就是bitmap数组下标的引用，例如某个边hash值计算的结果为100，则AFL就设置bitmap[100]非零，表示该边已经走过，所以需要确保bitmap size的值要大于边数。

在很多实际情况下的工程中，测试人员是只有二进制的程序，AFL原生提供了qemu的方式去fuzz二进制，但是效率太低，从哪方面考虑解决这个问题？

答：在AFL中，qemu，llvm，afl-gcc都是为了插桩得到edge的信息。而llvm和afl-gcc都是针对源代码，qemu是针对binary。qemu可视为一个虚拟机，目的是为了给binary提供运行环境，因为binary的插桩其实是比较困难的，所以直接用qemu的运行状态来得到fuzzing想要的插桩效果，这些操作本质都是给插桩服务的。因此如果要解决qemu的速度问题，本质就是要找到合适的binary插桩方式，或者找到更好的“虚拟机”。

以上两个问题感谢师兄解答