目录
写在前面
本文是对于机器学习中SVM算法的一次学习记录,主要介绍SVM的原理和简单应用。通过自己实际操作去理解SVM。
一. 绪论
1.1 什么是机器学习
机器学习并没有准确的权威定义,但作为机器学习领域的先驱Arthur Samuel将机器学习非正式定义为:“在不直接针对问题进行编程的情况下,赋予计算机学习能力的一个研究领域。”
因此,我们可以简单的理解为,机器学习这门学科所关注的问题是计算机程序如何随着经验的积累自动提高性能。
1.2 分类算法
分类算法是数据挖掘同时也是机器学习的一个重要技术之一,其应用遍及社会各个领域。分类任务就是通过学习得到一个目标函数(通常也称作分类模型,即分类器),把每个属性集映射到一个预先定义的类标号。分类和回归都可以用于预测。和回归方法不同的是,分类的类标号是离散属性,而预测建模的回归的目标属性是连续的。
构造分类器的过程一般分为训练和测试两个阶段。在构造模型之前,要求将数据集随机地分为训练数据集和测试数据集。在训练阶段,分析训练数据集的属性,为每个属性产生一个对相应数据集的属性描述或模型。在测试阶段,利用属性描述或模型对测试数据集进行分类,测试其分类准确度。一般来说,测试阶段的代价远远低于训练阶段。
为了提高分类的准确性、有效性和可伸缩性,在进行分类之前,通常要对数据进行预处理,包括:
(1)数据清理。其目的是消除或减少数据噪声,处理空缺值。
(2)相关性分析。由于数据集中的许多属性可能与分类任务不相关,若包含这些属性将减慢和可能误导学习过程。相关性分析的目的就是删除这些不相关或冗余的属性。
(3)数据变换。数据可以概化到较高层概念。比如,连续值属性“收入”的数值可以概化为离散值:低,中,高。又比如,标称值属性“市”可概化到高层概念“省”。此外,数据也可以规范化, ,规范化将给定属性的值按比例缩放,落入较小的区间,比如[0,1]等。
分类模型的构造方法有决策树类、基于规则类、最近邻类、贝叶斯类、人工神经网络类等。
二. 支持向量机SVM
2.1 SVM的基本概念
支持向量机( support vector machine ),简称SVM,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
2.2 SVM的基本思想
SVM可以分为两个部分了解。
一什么是支持向量,简单来说,就是支持或支撑平面上把两类类别划分开来的超平面的向量点。
二这里的“机”是什么意思,这里的“机(machine,机器)”便是一个算法。在机器学习领域,常把一些算法看做是一个机器,如分类机(当然,也叫做分类器),而支持向量机本身便是一种监督式学习的方法,它广泛的应用于统计分类以及回归分析中。
支持向量机(SVM)是90年代中期发展起来的基于统计学习理论的一种机器学习方法,通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。
我们可以通过几个例子来理解SVM的基本思想。

图2.1
如图2.1,图中存在两种颜色的球,需要我们使用一条线将其分开。如图2.2。
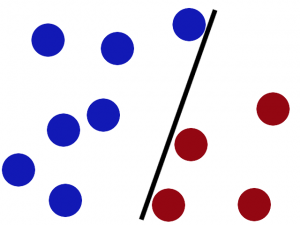
图2.2
这似乎没有什么难度,但是如果我们再继续添加一些球,那么此时该条线可能就不是那么的适用了。如图2.3。
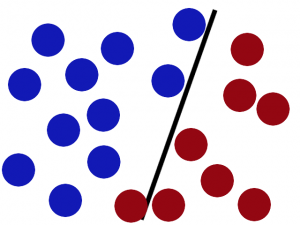
图2.3
这时,SVM就派上了用场。我们利用SVM方法将该条线放在最佳的位置,好让在这条线的两边有尽可能大的空间。如图2.4、图2.5.
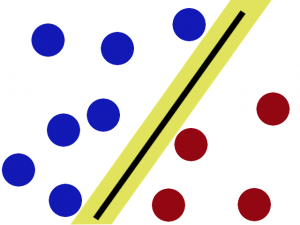
图2.4
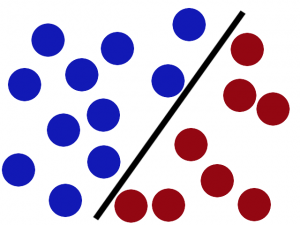
图2.5
即使是在原有的基础上加上一些球,该条线也是最佳的位置。但是SVM算法的思想不仅仅于此,如果上图中的蓝球和红球混合(如图2.6),又该如何处理呢?

图2.6
这时就可以利用SVM中的一个重要trick,将该图假象在空间中,我们的视角是从上往下看,这样一来,一定会存在与上文中提到的“线”类似的“面”,如图2.7所示。
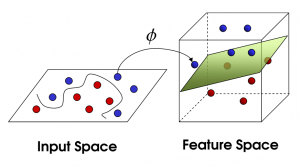
图2.7
当该面出现后,我们再俯视观察,可以看到图2.8所示。
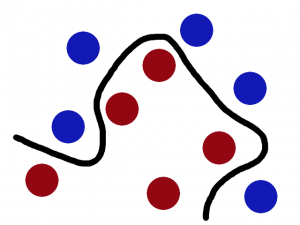
图2.8
于是这个时候,我们可以将其转换为SVM的思想。这些“球”可以视为data(数据),“线”可以视为classifier(分类器),最大间隙可以视为optimization(最优化),空间化的做法可以视为kernelling(核方法),而那个“面”则可以视为hyperplane(超平面)。
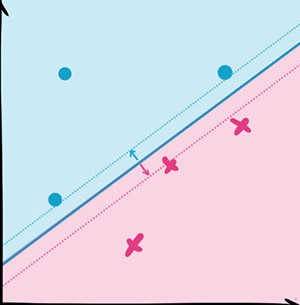
图2.9
如图2.9,其实SVM的核心思想就是找到不同类别之间的分界面,使得两类样本尽量落在面的两边,而且离分界面尽量远。最早的SVM是平面的,局限很大。但是利用核函数(kernel function),我们可以把平面投射(mapping)成曲面,进而大大提高SVM的适用范围。
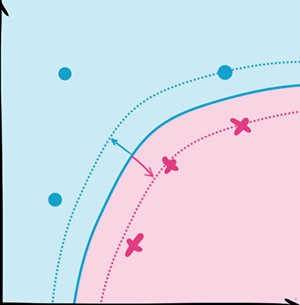
图2.10
提高之后的SVM同样被大量使用,在实际分类中展现了很优秀的正确率。
2.3 SVM的常见模型
SVM的常见模型可以分为两种,一种是线性支持向量机,一种是非线性支持向量机。本文主要介绍线性支持向量机中的软间隔最大化模型,在介绍这种模型前,首先要了解什么是支持向量以及SVM模型的目标函数。
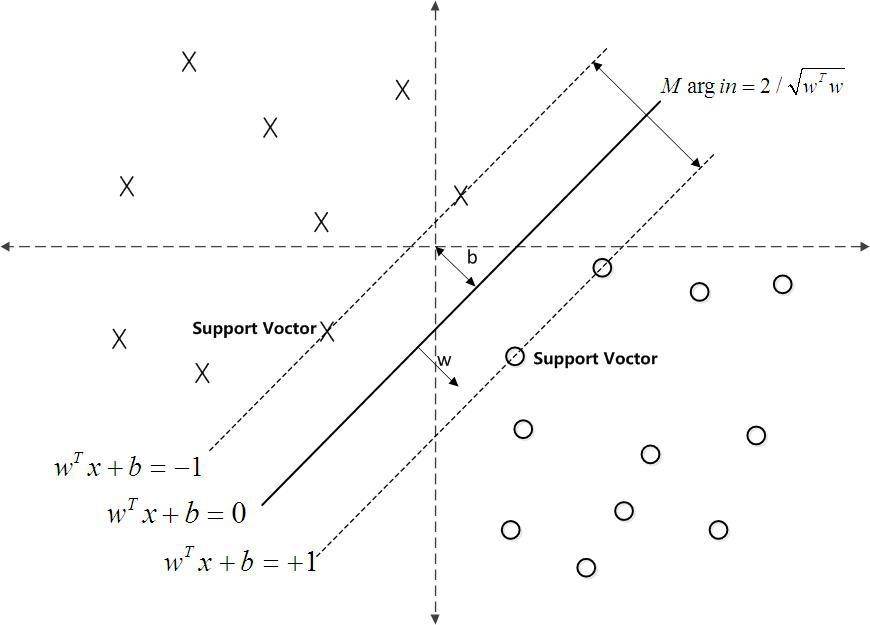
图2.11

公式中各符号的含义为:
对于有些测试实例,代入以上公式,按得出结果的正负号来进行分类。
但是在线性支持向量机中,存在某些情况,例如有时候线性数据集里面多了少量的异常点,由于这些异常点导致了数据集不能线性可分,如图2.12。
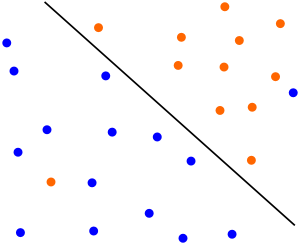
图2.12
除此之外,还有一种情况没有这么糟糕到不可分,但是会严重影响我们模型的泛化预测效果,比如图2.13,本来如果我们不考虑异常点,SVM的超平面应该是下图中的红色线所示,但是由于有一个蓝色的异常点,导致我们学习到的超平面是下图中的粗虚线所示,这样会严重影响我们的分类模型预测效果。
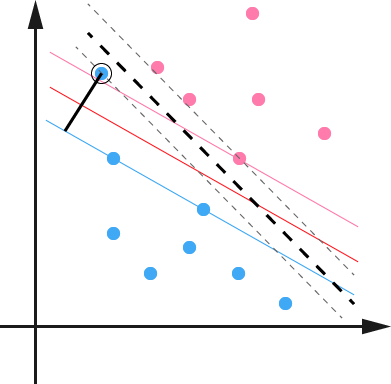
图2.13
正式由于这种情况,SVM引入了软间隔最大化的模型来解决。
所谓的软间隔[7],是相对于硬间隔说的,我们可以认为上文中提到的公式(2)为硬间隔的最大化的条件。SVM对于训练集里面的每个样本(x_i,y_i )引入了一个松弛变量ξ_i≥0,使函数间隔加上松弛变量大于等于1,也就是说:

其实,如果将软间隔看成空间化,那么会更好理解。对于图2.12的情况,可以通过以下两个步骤解决:
利用一个非线性的映射把原数据集中的向量点转化到一个更高维度的空间中
在这个高纬度的空间中找一个线性的超平面来进行可区分处理
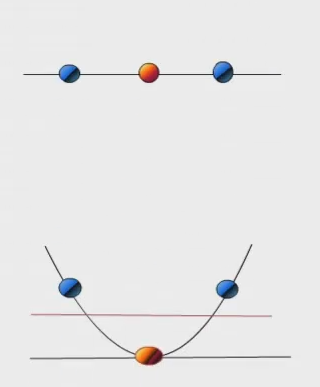
图2.14
如图2.14所示,将其从一维转为二维空间,然后在二维空间进行求解。
三. 支持向量机SVM的应用
3.1 模型可视化展示
在本例子中,我们主要利用python的sklearn库来描绘出超平面,进行可视化展示。
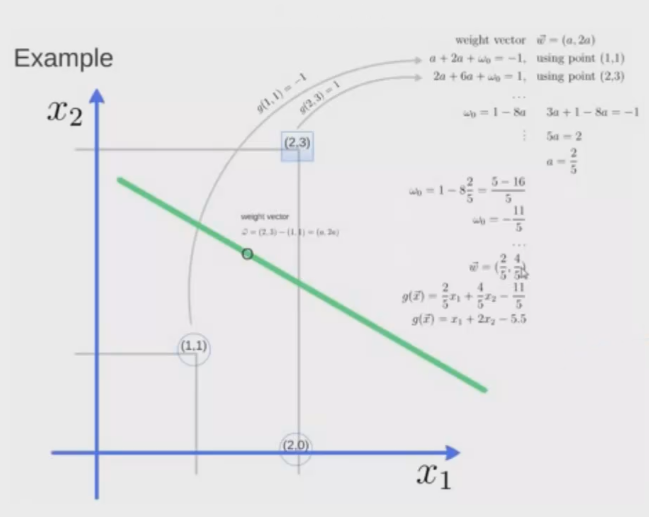
图3.1
如图3.1,在二维空间中,有三个点:(1, 1) (2, 0) (2, 3) 。前两个点属于一类,第三个点属于另一类。可以确定的是,有两个点是支持向量:(1, 1) (2, 3),因此通过sklearn库中的 support_vectors_ 可以得到具体的点,具体编程实例如图3.2。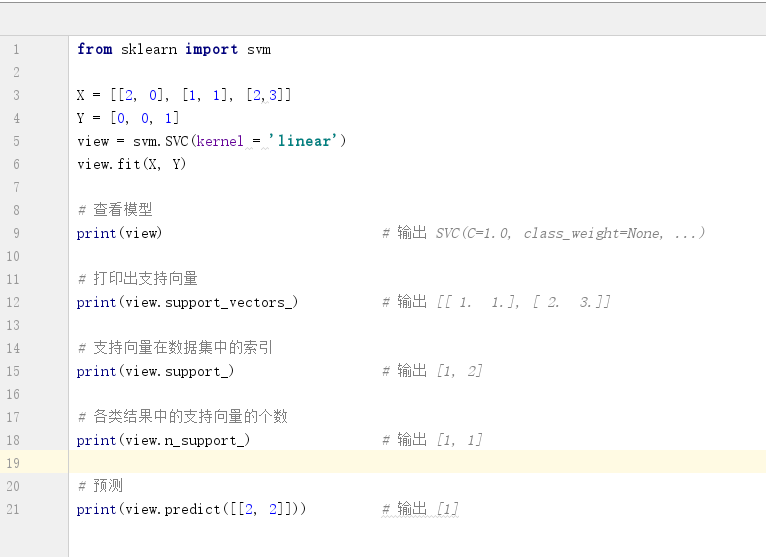
图3.2
运行结果,如图3.3.

图3.3
由于分界线的两侧各有一个支持向量,因此 view.n_support_ 的结果为 [1, 1]。与此类似,我们可以通过提高点的个数,将超平面画出来,进行可视化展示。具体步骤如下:
构造模型
收集数据
取点,找出目标线
绘图

具体编程实例如图3.4。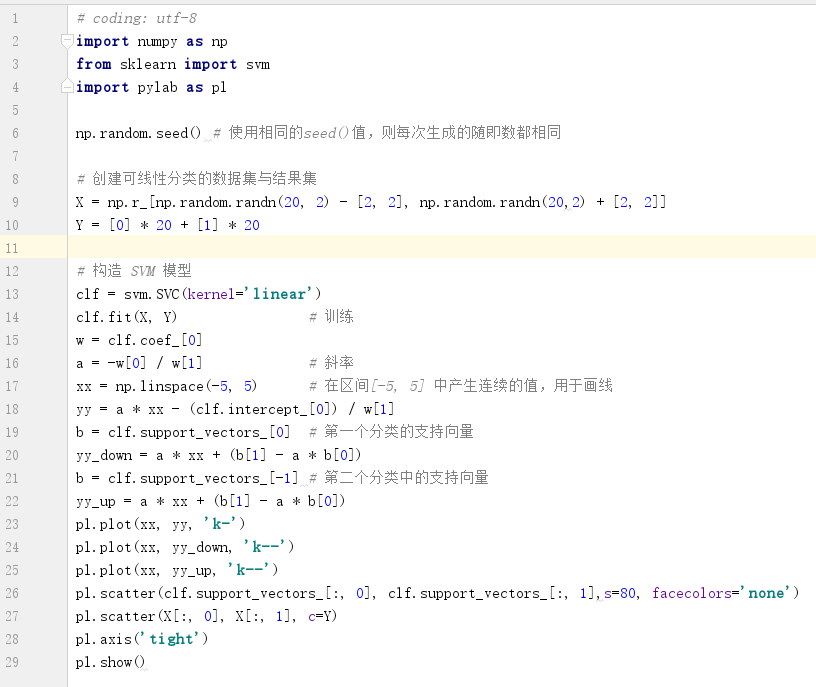
图3.4
# coding: utf-8
import numpy as np
from sklearn import svm
import pylab as pl
np.random.seed() # 使用相同的seed()值,则每次生成的随即数都相同
# 创建可线性分类的数据集与结果集
X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20,2) + [2, 2]]
Y = [0] * 20 + [1] * 20
# 构造 SVM 模型
clf = svm.SVC(kernel='linear')
clf.fit(X, Y) # 训练
w = clf.coef_[0]
a = -w[0] / w[1] # 斜率
xx = np.linspace(-5, 5) # 在区间[-5, 5] 中产生连续的值,用于画线
yy = a * xx - (clf.intercept_[0]) / w[1]
b = clf.support_vectors_[0] # 第一个分类的支持向量
yy_down = a * xx + (b[1] - a * b[0])
b = clf.support_vectors_[-1] # 第二个分类中的支持向量
yy_up = a * xx + (b[1] - a * b[0])
pl.plot(xx, yy, 'k-')
pl.plot(xx, yy_down, 'k--')
pl.plot(xx, yy_up, 'k--')
pl.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],s=80, facecolors='none')
pl.scatter(X[:, 0], X[:, 1], c=Y)
pl.axis('tight')
pl.show()
我们可以通过改变seed()种子的值,来描绘出不同分布的数据进行绘图。如图3.5、3.6、3.7所示。
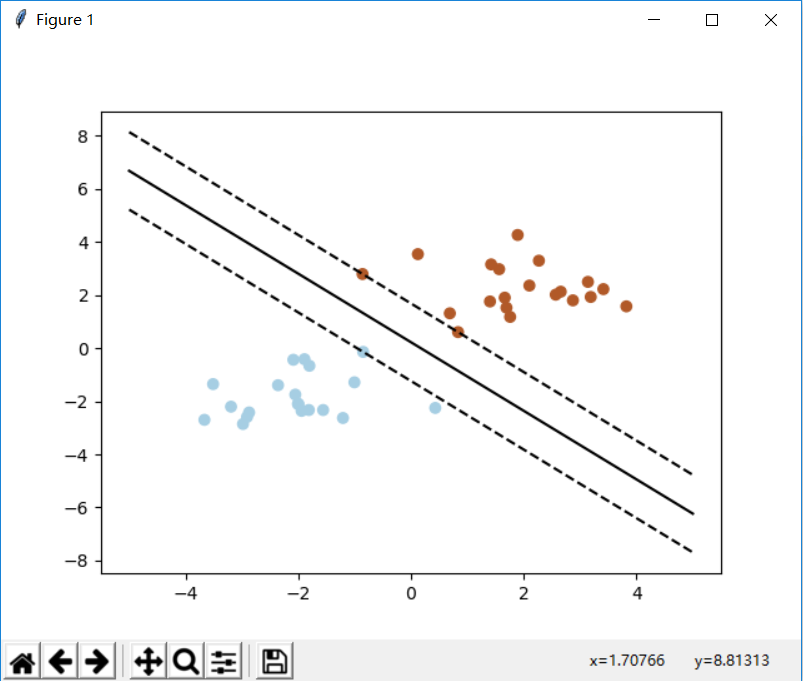
图3.5
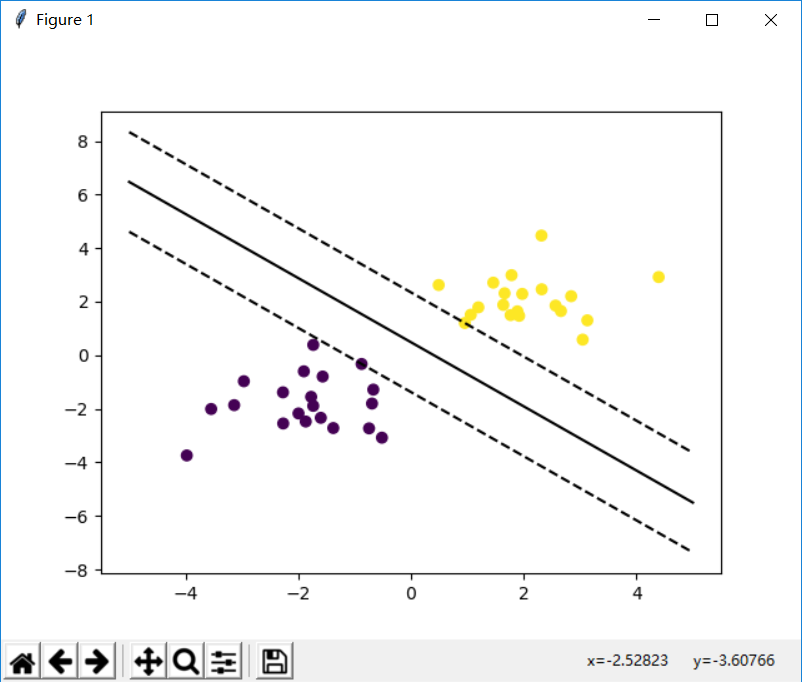
图3.6
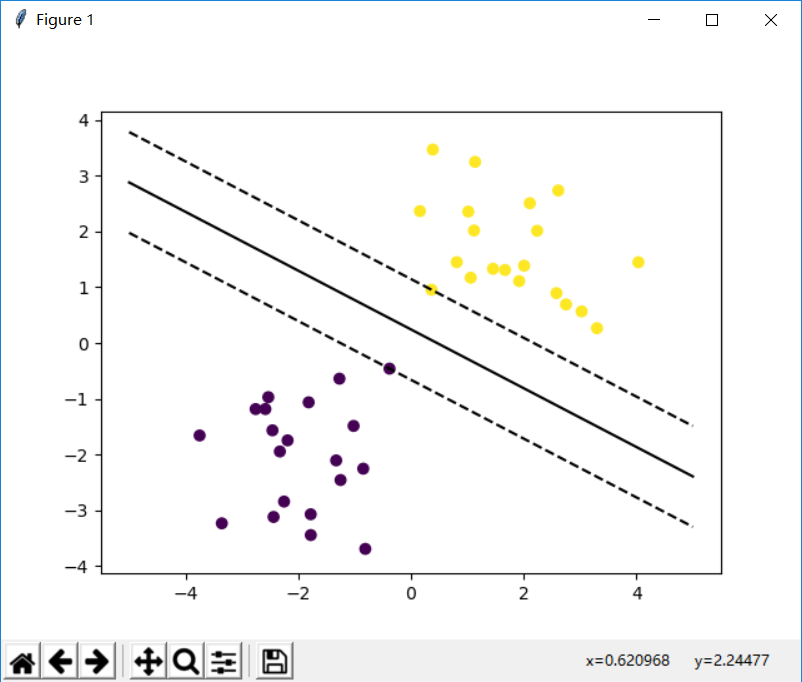
图3.7
3.2 人脸识别
本算法流程就是用主成分分析(Pca)对人脸数据集进行降维,得到数个人脸特征向量。对于任意一个人脸样本,将样本数据向特征向量投影,得到的投影系数作为人脸的特征表示。使用支持向量机(SVM)对这些不同的投影系数向量分类,来进行人脸识别。
主要步骤如下:
(1)人脸数据集基本信息
本次测试使用的是英国剑桥大学AT&T人脸数据集,该数据集大小为4.68M,有40类样本,每类中包含同一个人的10张图像。
(2)拆分训练集和测试集
我们首先读入数据集,将每一幅图像拉成一列,组成数据集合(112*92,400),并保存每一列数据对应的人脸标号,以及原图的高度和宽度,为了处理后还原显示。将数据集分成训练集和测试集,这样的好处是,不用额外找图片作为测试集,而且从数据集中分离的数据,是包含分类结果的,这样有利于我们对结果预测的对比。
利用 sklearn 中提供的 train_test_split 可以进行这样的划分:
X_train, X_test, Y_train, Y_test = train_test_split(X, Y,
test_size=0.25)
这个函数返回四个结果,训练集特征向量,测试集特征向量,训练集归类标记,测试集归类标记。
(3)特征降维处理
原始数据的特征向量维度是非常高的(1859维),这就意味着,训练模型的复杂度非常高,因此,需要通过一定的手段将特征值进行降维操作,来提高性能。有时降维处理后的数据,反而能提高准确性,这是因为可以减少噪点带来的影响。
(4)提取特征点
提取人脸中的特征点,以供于后续的图像可视化。
(5)构造SVM分类器
因为我们不知道哪些参数会产生最好的结果,因此使用不同的参数来训练,然后选取训练最好的模型。进行多个量的尝试后,进行搜索,选出准确率最高的模型。
(6)预测
得到预测结果中,哪些是正确哪些是错误的。
(7)测试结果可视化
将测试的结果进行展示,原先图片应该是谁,结果预测成谁。
本次测试主要实例代码如下:
from __future__ import print_function
from time import time
import logging
import matplotlib.pyplot as plt
import cv2
from numpy import *
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
from sklearn.svm import SVC
#读取图像
PICTURE_PATH = "F:\\face\\"
def get_Image():
for i in range(1,41):
for j in range(1,11):
path = PICTURE_PATH + "\\s" + str(i) + "\\"+ str(j) + ".pgm"
img = cv2.imread(path)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
h,w = img_gray.shape
img_col = img_gray.reshape(h*w)
all_data_set.append(img_col)
all_data_label.append(i)
return h,w
all_data_set = []
all_data_label = []
h,w = get_Image()
X = array(all_data_set)
y = array(all_data_label)
n_samples,n_features = X.shape
n_classes = len(unique(y))
target_names = []
for i in range(1,41):
names = "person" + str(i)
target_names.append(names)
print("Total dataset size:")
print("n_samples: %d" % n_samples)
print("n_features: %d" % n_features)
print("n_classes: %d" % n_classes)
# 拆分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=42)
# 特征降维处理
n_components = 20
print("Extracting the top %d eigenfaces from %d faces"% (n_components, X_train.shape[0]))
t0 = time()
pca = PCA(n_components=n_components, svd_solver='randomized',whiten=True).fit(X_train) #选择一种svd方式
print("done in %0.3fs" % (time() - t0))
eigenfaces = pca.components_.reshape((n_components, h, w)) #特征脸
print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
X_train_pca = pca.transform(X_train) #得到训练集投影系数
X_test_pca = pca.transform(X_test) #得到测试集投影系数
print("done in %0.3fs" % (time() - t0))
print("Fitting the classifier to the training set")
t0 = time()
param_grid = {'C': [1e3, 5e3, 1e4, 5e4, 1e5], 'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], }
clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid)
#class_weight='balanced'表示调整各类别权重,权重与该类中样本数成反比,
#防止模型过于拟合某个样本数量过大的类
clf = clf.fit(X_train_pca, y_train)
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_)
print("Predicting people's names on the test set")
t0 = time()
y_pred = clf.predict(X_test_pca)
print("done in %0.3fs" % (time() - t0))
print(classification_report(y_test, y_pred, target_names=target_names))
print(confusion_matrix(y_test, y_pred, labels=range(n_classes)))
def plot_gallery(images, titles, h, w, n_row=3, n_col=4):
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(images[i].reshape((h, w)))
plt.title(titles[i], size=12)
plt.xticks(())
plt.yticks(())
def title(y_pred, y_test, target_names, i):
pred_name = target_names[y_pred[i]-1]
true_name = target_names[y_test[i]-1]
return 'Predicted: %s\nResult: %s' % (pred_name, true_name)
prediction_titles = [title(y_pred, y_test, target_names, i)for i in range(y_pred.shape[0])]
eigenface_titles = ["Eigenface %d" % i for i in range(eigenfaces.shape[0])]
plot_gallery(X_test, prediction_titles, h, w)
plot_gallery(eigenfaces, eigenface_titles, h, w)
plt.show()
运行实例后,首先会会得到训练集、测试集在特征向量的投影系数以及SVM分类器,如图3.8.
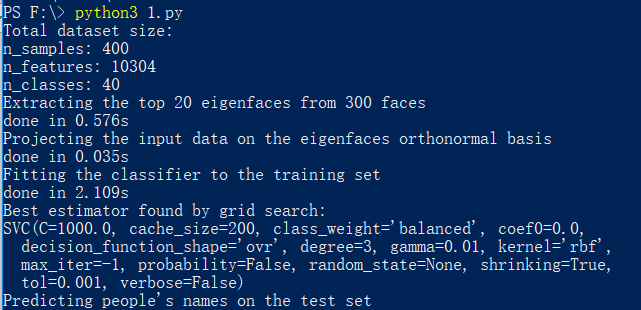
图3.8
除此之外,还会生成一个含有查准率(precision)、查全率(recall)、F1值(f1-score)以及测试样本数的数据表,如图3.9。
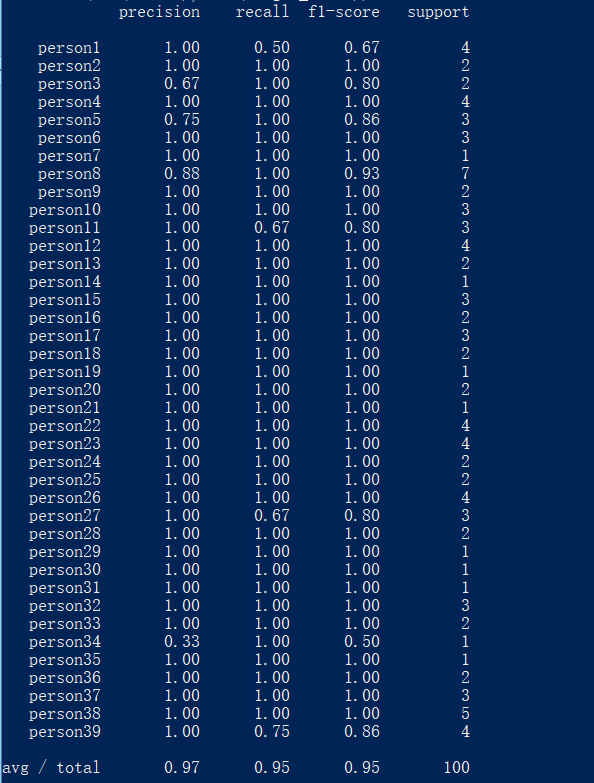
图3.9
最后得到特征脸集合以及预测的结果集,如图3.10、3.11。
图3.10

图3.11
由图3.11可以看到,大部分的预测还是对的,图3.10是由特征点抽象而成的特征脸,这是一个抽象化的对特征的提取,虽然对人来说它的辨识度低,但对机器来说是很有帮助的。
四. 支持向量机SVM的优劣分析
4.1 SVM的优点
SVM的主要优点包括:
它是专门针对有限样本情况的,其口标是得到现有信息下的最优解,而不仅仅是样本数口趋于无穷大时的最优值;
算法最终转化为一个二次型寻优问题。从理论上说,得到的将是全局最优点,解决了在神经网络方法中无法避免的局部极值问题;
算法将实际问题通过非线性变换到高维的特征空间,在高维空间中构造线性判别函数以替换原空间中的非线性判别函数,这样能保证机器有较好的推广能力,同时它巧妙地解决了维数问题,算法复杂度与样本维数无关。
4.1 SVM的劣势
目前SVM研究中仍需要解决的一些难点,包括如下的一些方面:
核函数和参数的构造和选择缺乏理论指导。核函数的选择影响着分类器的性能,如何根据待解决问题的先验知识和实际样本数据,选择和构造合适的核函数、确定核函数的参数等问题,都缺乏相应的理论指导。
训练大规模数据集的问题。如何解决训练速度与训练样本规模间的矛盾,测试速度与支持向量数口间的矛盾,找到对大规模样本集有效的训练算法和分类实现算法,仍是未很好解决的问题。
多类分类问题的有效算法与SVM优化设训一问题。尽管训练多类SVM问题的算法已被提出,但用于多类分类问题时的有效算法、多类SVM的优化设计仍是一个需要进一步研究的问题。
四. 总结
机器学习中分类算法的种类还有很多,如:决策树分类算法、基于规则分类算法、贝叶斯分类算法以及人工神经网络算法等。
本文主要讨论了支持向量机SVM算法。SVM的重要理论基础是统计学习理论的VC维理论和结构风险最小化原理。SVM根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷,以期获得最好的推广能力。SVM可以自动寻找对分类有较好区分能力的支持向量,由此构成的分类器可以最大化类与类之间的间隔。但同时,SVM也比较依赖大规模的训练数据集,如何获取大量的训练数据集以及如何解决训练速度和训练样本规模间的矛盾仍是存在的问题。
总之,SVM算法有很多成功的应用领域,如人脸识别、手写体识别、指纹识别等。这些应用都说明了基于VC维理论和结构风险最小化原理而发展起来的结构化学习方法的潜在优势。
相关下载
链接:https://pan.baidu.com/s/1slE7s2h
密码:kdn7
参考:
[1] 刘红岩,陈剑,陈国青. 数据挖掘中的数据分类算法综述
[2] 陶卿,曹进德,孙德敏. 基于支持向量机分类的回归方法
[3] 罗海蛟,刘显.数据挖掘中分类算法的研究及其应用
[4] Iddo. Support Vector Machines explained well
[5] Nello Cristianini,John Shawe-Taylor. 支持向量机导论
[6] 邓乃扬,田英杰. 数据挖掘中的新方法:支持向量机
[7] 林轩田. 机器学习技法. MOOC
[8] 段纪军,陈琳,王海燕,田娜.基于数据挖掘技术与支持向量机的目标识别研究
[9] 朱凌云,曹长修.基于支持向量机的缺陷识别方法
[10] Support Vector Machines explained well
[11] 支持向量机(SVM)是什么意思?
[12] svm 算法通俗介绍
[13] 分类算法之支持向量机:SVM(应用篇)
[14] Scikit-learn实例之Pca+Svm人脸识别(AT&T数据集)
 panda
panda 

暂时无法评论哦~
暂无评论